Tautology In Discrete Mathematics
In this blog I am going to explain Tautology in Discrete Mathematics. First of all we will discuss what is tautology? Then I will give you some Examples of Tautology that How to check Tautology?.
So let's Start discussion..
What is Tautology?
A compound Proposition which is always true, is called a Tautology.
Here, Firstly we have to understand the meaning of two words "Compound" and "Proposition".
Propositions:-
Declarative sentence that is either true or False, but not both is called Proposition. For example
- 2+3=5 , this statement always gives true value so it is propositional statement.
- same as X is vowel , this statement always gives false value so it is also propositional statement.
- And What time is it? also X+1=2 both statements are indeterminate statements so it is not a propositional statement.
Now the definition of tautology said compound proposition mean a propositional statement connected with another propositional statement whose overall result/ value is true then that compound proposition is called Tautology.
For connecting proposition statements we required logical connectives or in another ways Propositions are joined together by logical connectives. some of them are-
- Disjunction/ OR (∨)
- Conjunction/ AND (∧)
- Negation/ NOT (¬)
- Conditional / if-then (→)
- Biconditional/ If and only if (⇔)
Example-1
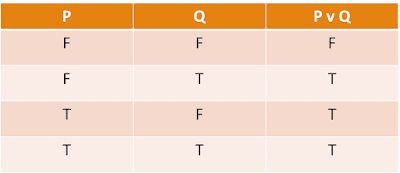
Find if P v Q is a tautology or not?
Solution:- Here P and Q are two proposition statements , we create a truth table by taking all the possible combination of P and Q 's values such as
Here P and Q are two statements so there are only four possible values and p and q are connected with Disjunction/ OR operator (Rule:- if at least one statement is true then it gives true) so when P and Q both are false this operator gives false value but for making statement tautology needed all values true. Therefore, it is not a tautology
Here P and Q are two statements so there are only four possible values and p and q are connected with Disjunction/ OR operator (Rule:- if at least one statement is true then it gives true) so when P and Q both are false this operator gives false value but for making statement tautology needed all values true. Therefore, it is not a tautology
Related Other Post
- Cloud Computing Introduction
- DBMS Tutorial
- Data Structure Tutorial
- Service Oriented Architecture
- OSI Model
- Artificial intelligence Tutorial
Example-2
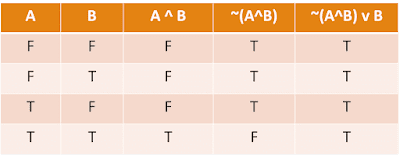
Show that ¬(A ∧ B) V ASolution:-Here A and B are two proposition statements , we create a truth table by taking all the possible combination of A and B 's values such as
Here A and B are two statements so there are only four possible values and A and B are connected with Multiple Operator so after performing multiple operation finally gives true values in each case. Therefore, it is a tautology.


0 Comments
if u have any doubts please let me know,