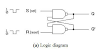
A* Search Algorithm:-
A* search is the most commonly known
form of best-first search. It uses heuristic function h(n), and cost to reach
the node n from the start state g(n). It has combined features of UCS and
greedy best-first search, by which it solve the problem efficiently. A* search
algorithm finds the shortest path through the search space using the heuristic
function. This search algorithm expands less search tree and provides optimal
result faster. A* algorithm is similar to UCS except that it uses g(n)+h(n)
instead of g(n).
Algorithm of A* search:
Step1: Place the starting node in the OPEN list.
Step 2: Check if the OPEN list is empty or not, if the
list is empty then return failure and stops.
Step 3: Select the node from the OPEN list which has
the smallest value of evaluation function (g+h), if node n is goal node then
return success and stop, otherwise
Step 4: Expand node n and generate all of its
successors, and put n into the closed list. For each successor n', check
whether n' is already in the OPEN or CLOSED list, if not then compute
evaluation function for n' and place into Open list.
Step 5: Else if node n' is already in OPEN and CLOSED,
then it should be attached to the back pointer which reflects the lowest g(n')
value.
Step 6: Return to Step 2.
Advantages:
- A* search algorithm is the best algorithm than other search algorithms.
- A* search algorithm is optimal and complete.
- This algorithm can solve very complex problems.
Disadvantages:
- It does not always produce the shortest path as it mostly based on heuristics and approximation.
- A* search algorithm has some complexity issues.
- The main drawback of A* is memory requirement as it keeps all generated nodes in the memory, so it is not practical for various large-scale problems.
Example:
In this example, we will traverse the given graph using the
A* algorithm. The heuristic value of all states is given in the below table so
we will calculate the f(n) of each state using the formula f(n)= g(n) + h(n),
where g(n) is the cost to reach any node from start state.Here we will use OPEN
and CLOSED list.
Initialization: {(S, 5)}
Iteration1: {(S--> A, 4), (S-->G, 10)}
Iteration2: {(S--> A-->C, 4), (S--> A-->B,
7), (S-->G, 10)}
Iteration3: {(S--> A-->C--->G, 6), (S-->
A-->C--->D, 11), (S--> A-->B, 7), (S-->G, 10)}
Iteration 4 will give the final result,
as S--->A--->C--->G it provides the optimal path with cost
6.
- Complete: A* algorithm is complete as long as:Branching factor is finite.
- Optimal: A* search algorithm is optimal
- Time Complexity: The time complexity of A* search algorithm depends on heuristic function, and the number of nodes expanded is exponential to the depth of solution d. So the time complexity is O(b^d), where b is the branching factor.
- Space Complexity: The space complexity of A* search algorithm is O(b^d)





0 Comments
if u have any doubts please let me know,