Prim's Spanning Tree Algorithm:-
- Prim's algorithm to find minimum cost spanning tree.
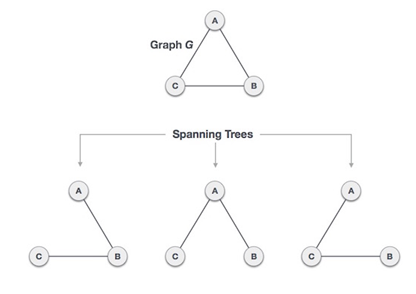
- A Spanning Tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges.
- A spanning tree does not have cycles and it cannot be disconnected.
- In a weighted graph, a Minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph.
- Prim's algorithm shares a similarity with the shortest path first algorithms.
- Prim’s algorithm is also a Greedy algorithm.
Algorithm:-
Step 1 - Remove all loops and parallel edgesStep 2 - Choose any arbitrary node as root node
Step 3 - Check outgoing edges and select the one with less cost.
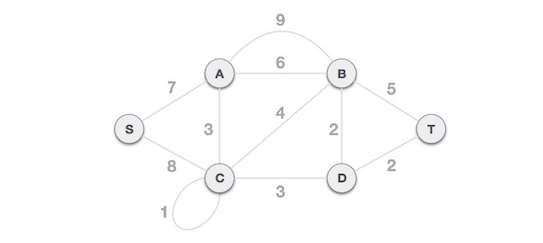
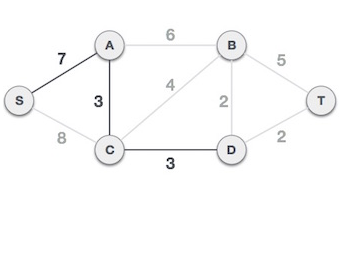
Example:-
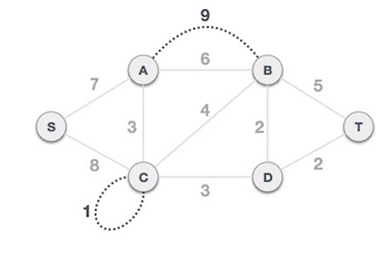
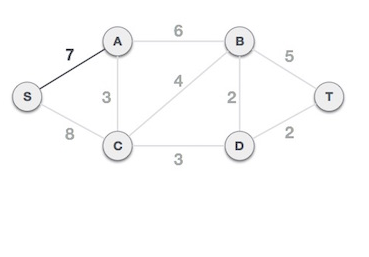
Step-1 firstly we remove all parallel edges and self loop, in above example there are one self loop and one parallel edge ( as mentioned using dotted line below)Step-2 choose S as root node( we can choose any node as root node).now choose an edge starting from S Node having less weight or value, i.e. S-A (7)
Step-3 Choose another edge having less value starting from either A or S. here we choosen edge A-C (3)
Step-4 next least cost edge is C-D (3), vertex D is added in our spanning tree
Step 5:- from Vertex D there are two edges having same value that is 2, choosen both edges and connected vertices B and T with vertex D.
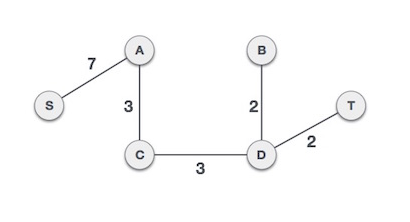
finally our minimum spanning tree( MST) is as show bellow
Applications of Minimum Spanning Tree:-
- Network design:- The standard application is to a problem like phone network design. we have a business with several offices; we want to lease phone lines to connect them up with each other; and the phone company charges different amounts of money to connect different pairs of cities. we want a set of lines that connects all our offices with a minimum total cost. It should be a spanning tree, since if a network isn’t a tree you can always remove some edges and save money.
- Traveling salesperson problem:-Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city.


0 Comments
if u have any doubts please let me know,