First-Order Logic in Artificial intelligence:-
in propositional logic, we can only represent the facts,
which are either true or false. PL is not sufficient to represent the complex
sentences or natural language statements. The propositional logic has very
limited expressive power. Consider the following sentence, which we cannot
represent using PL logic.
"Some humans are intelligent", or
"Sachin likes cricket."
To represent the above statements, PL logic is not
sufficient,it can be represented using FOL.
First-Order logic:
- First-order logic is another way of knowledge representation in artificial intelligence. It is an extension to propositional logic.
- FOL is sufficiently expressive to represent the natural language statements in a concise way.
- First-order logic is also known as Predicate logic or First-order predicate logic. First-order logic is a powerful language that develops information about the objects in a more easy way and can also express the relationship between those objects.
- First-order logic (like natural language) does not only assume that the world contains facts like propositional logic but also assumes the following things in the world:
- Objects: A, B, people, numbers, colors, wars, theories, squares, pits, wumpus, ......
- Relations: It can be unary relation such as: red, round, is adjacent, or n-any relation such as: the sister of, brother of, has color, comes between
- Function: Father of, best friend, third inning of, end of, ......
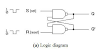
Syntax of First-Order logic:
The syntax of FOL determines which collection of symbols is
a logical expression in first-order logic. The basic syntactic elements of
first-order logic are symbols. We write statements in short-hand notation in
FOL.
Atomic sentences:
Atomic sentences are the most basic sentences of first-order
logic. These sentences are formed from a predicate symbol followed by a
parenthesis with a sequence of terms.We can represent atomic sentences
as Predicate (term1, term2, ......, term n).
Example:
Ravi and Ajay are brothers: => Brothers(Ravi,
Ajay).
Chinky is a cat: => cat (Chinky).
Chinky is a cat: => cat (Chinky).
Complex Sentences:
Complex sentences are made by combining atomic sentences
using connectives. First-order logic statements can be divided into two parts:
Subject: Subject is the main part of the statement.
Predicate: A predicate can be defined as a relation,
which binds two atoms together in a statement.
Consider the statement: "x is an integer.", it
consists of two parts, the first part x is the subject of the statement and
second part "is an integer," is known as a predicate.
Quantifiers in First-order logic:
These are the symbols that permit to determine or identify
the range and scope of the variable in the logical expression. There are two
types of quantifier:
Universal Quantifier, (for all, everyone, everything)
Existential quantifier, (for some, at least one).
Universal Quantifier:
Universal quantifier is a symbol of logical representation,
which specifies that the statement within its range is true for everything or
every instance of a particular thing.The Universal quantifier is represented by
a symbol ∀, which resembles an inverted A.
If x is a variable, then ∀x is read as:
For all x For
each x For
every x.
Example:-
All man drink coffee.
Let a variable x which refers to a man so all x can be
represented as
∀x man(x) → drink (x, coffee).
It will be read as: There are all x where x is a man who
drink coffee.
Existential Quantifier:
Existential quantifiers are the type of quantifiers, which express
that the statement within its scope is true for at least one instance of
something.It is denoted by the logical operator ∃
If x is a variable, then existential quantifier will be ∃x
or ∃(x).
And it will be read as: There
exists a 'x.' For some 'x.' For at least one 'x.'
Example:
Some boys are intelligent.
∃x: boys(x) ∧ intelligent(x)
It will be read as: There are some x where x is a boy who is
intelligent.


0 Comments
if u have any doubts please let me know,